02. 퍼셉트론
이 글은 '밑바닥부터 시작하는 딥러닝' 이란 책으로 공부하며 작성했다.
2.1 퍼셉트론이란?
퍼셉트론: 다수 신호를 입력받아 하나 신호 출력
퍼셉트론 신호: 흐르는 정보. 흐른다(1)/안 흐른다(0).

'뉴런이 활성화한다': 뉴런에서 보낸 신호의 총합이 임계값(θ)을 넘으면 1을 출력한다.
뉴런의 가중치↑ 신호의 중요도↑ (저항↓)
<정리>

2.2 단순한 논리 회로
AND 게이트: 입력 2, 출력 1. 둘 다 1이면 1 출력.
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
위를 만족하려면 θ>0, x1≤θ, x2≤θ, x1+x2>θ이여야 한다.
NAND 게이트: AND의 반대.
| x1 | x2 | y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
위를 만족하려면 AND의 반대인 θ<0, x1>θ, x2>θ, x1+x2 <θ이여야 한다.
OR 게이트: 입력 신호 중 최소 1개 1이면 1 출력.
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
위를 만족하려면 θ>0, x1>θ, x2>θ이여야 한다.
AND, NAND, OR 게이트의 퍼셉트론 구조는 동일하며, 가중치와 임계값에 따라 달라진다.
2.3 퍼셉트론 구현하기
논리회로를 1 챕터에서 배원 파이썬으로 구현한다.
def AND(x1,x2):
w1,w2,theta = 0.5,0.5,0.7
tmp = x1*w1 + x2*w2
if tmp<=theta:
return 0
else:
return 1
print(AND(0,0)) # 0
print(AND(0,1)) # 0
print(AND(1,0)) # 0
print(AND(1,1)) # 1
위의 <정리>에 θ=-b를 대입하면 아래와 같다. b를 편향(bias)라고 한다.
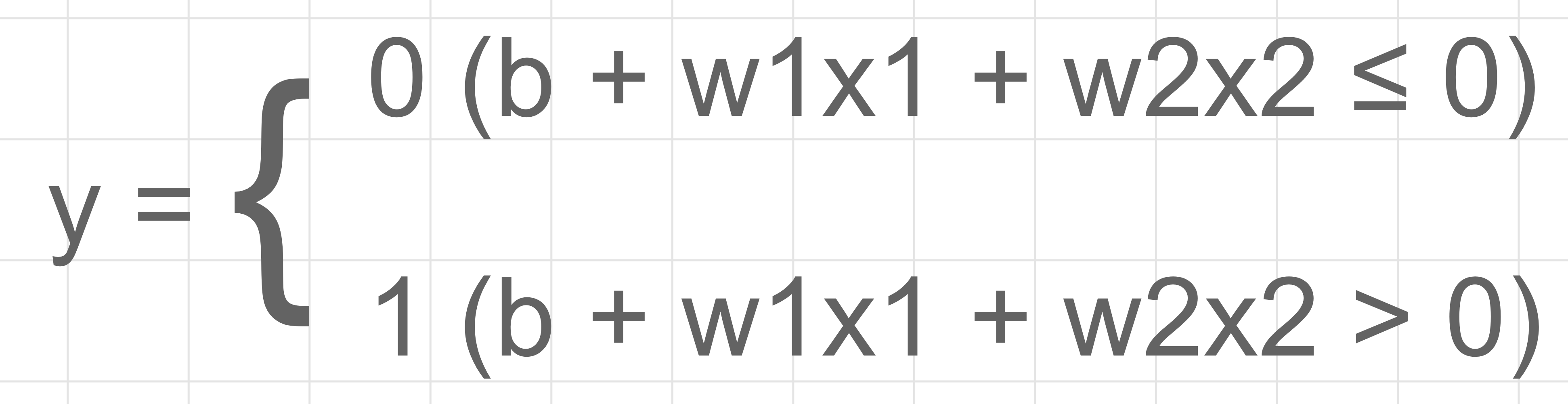
이를 통해 정리하면 아래와 같다.
if 입력신호*가중치+편향>0 : 1
else : 0>>> import numpy as np
>>> x = np.array([0,1]) # 입력 신호
>>> w = np.array([0.5,0.5]) # 가중치
>>> b = -0.7 # 편향
>>> w*x
array([0. , 0.5])
>>> np.sum(w*x)
0.5
>>> np.sum(w*x)+b
-0.19999999999999996 # 약 -0.2
가중치, 편향을 이용한 AND, NAND, OR 게이트를 구현한다.
#and.py
import numpy as np
def AND(x1,x2):
x=np.array([x1,x2])
w=np.array([0.5,0.5])
b=-0.7
tmp=np.sum(w*x)+b
if tmp<=0:
return 0
else:
return 1
print(AND(0,0)) # 0
print(AND(0,1)) # 0
print(AND(1,0)) # 0
print(AND(1,1)) # 1#nand.py
import numpy as np
def NAND(x1,x2):
x=np.array([x1,x2])
w=np.array([-0.5,-0.5]) # AND와 w,b 부호 반대
b=0.7
tmp=np.sum(w*x)+b
if tmp<=0:
return 0
else:
return 1
print(NAND(0,0)) # 1
print(NAND(0,1)) # 1
print(NAND(1,0)) # 1
print(NAND(1,1)) # 0#or.py
import numpy as np
def OR(x1,x2):
x=np.array([x1,x2])
w=np.array([0.5,0.5])
b=-0.2 # AND와 b만 다름
tmp=np.sum(w*x)+b
if tmp<=0:
return 0
else:
return 1
print(OR(0,0)) # 0
print(OR(0,1)) # 1
print(OR(1,0)) # 1
print(OR(1,1)) # 1
2.4 퍼셉트론의 한계
XOR(배타적 논리합) 게이트는 퍼셉트론으로 구현이 불가능하다.
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
좌표평면 위의 점으로 표현하면, (0,0), (1,1) / (0,1), (1,0)로, 직선 하나로 영역을 나눌 수 없다.
선형 영역(직선)이 아닌 비선형 영역(곡선)으로는 가능하다.
2.5 다층 퍼셉트론이 출동한다면
AND, NAND, OR을 조합해 XOR을 표현할 수 있다.
| x1 | x2 | NAND | OR | XOR |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
XOR = (x1 NAND x2) AND (x1 OR x2)
XOR의 다층 구조 퍼셉트론을 표현했다. 2층 퍼셉트론 (혹은 3층)
단층의 한계를 다층 구조로 구현 가능하다.

이를 구현하면 아래와 같다.
#xor.py
import numpy as np
def XOR(x1,x2):
return AND(NAND(x1,x2),OR(x1,x2))
def AND(x1,x2):
x=np.array([x1,x2])
w=np.array([0.5,0.5])
b=-0.7
tmp=np.sum(w*x)+b
if tmp<=0:
return 0
else:
return 1
def NAND(x1,x2):
x=np.array([x1,x2])
w=np.array([-0.5,-0.5])
b=0.7
tmp=np.sum(w*x)+b
if tmp<=0:
return 0
else:
return 1
def OR(x1,x2):
x=np.array([x1,x2])
w=np.array([0.5,0.5])
b=-0.2
tmp=np.sum(w*x)+b
if tmp<=0:
return 0
else:
return 1
print(XOR(0,0)) # 0
print(XOR(0,1)) # 1
print(XOR(1,0)) # 1
print(XOR(1,1)) # 0
2.6 NAND에서 컴퓨터까지
다층 퍼셉트론으로 가산기, 진수 인코더, 패리티 검사 회로, 컴퓨터를 표현할 수 있다.
이론상 2층 퍼셉트론이면 컴퓨터를 만들 수 있다.
(비선형인 시그모이드함수를 활성화 함수로 하면)