03. 신경망

Deep Learning

03. 신경망

huskycat1202 2021. 1. 24. 22:06

이 글은 '밑바닥부터 시작하는 딥러닝' 이란 책으로 공부하며 작성했다.

3.1 퍼셉트론에서 신경망으로

은닉층: 사람의 눈에 보이지 않는 뉴런으로 구성

편향의 입력 신호는 항상 1이다. (항상 입력된다.)

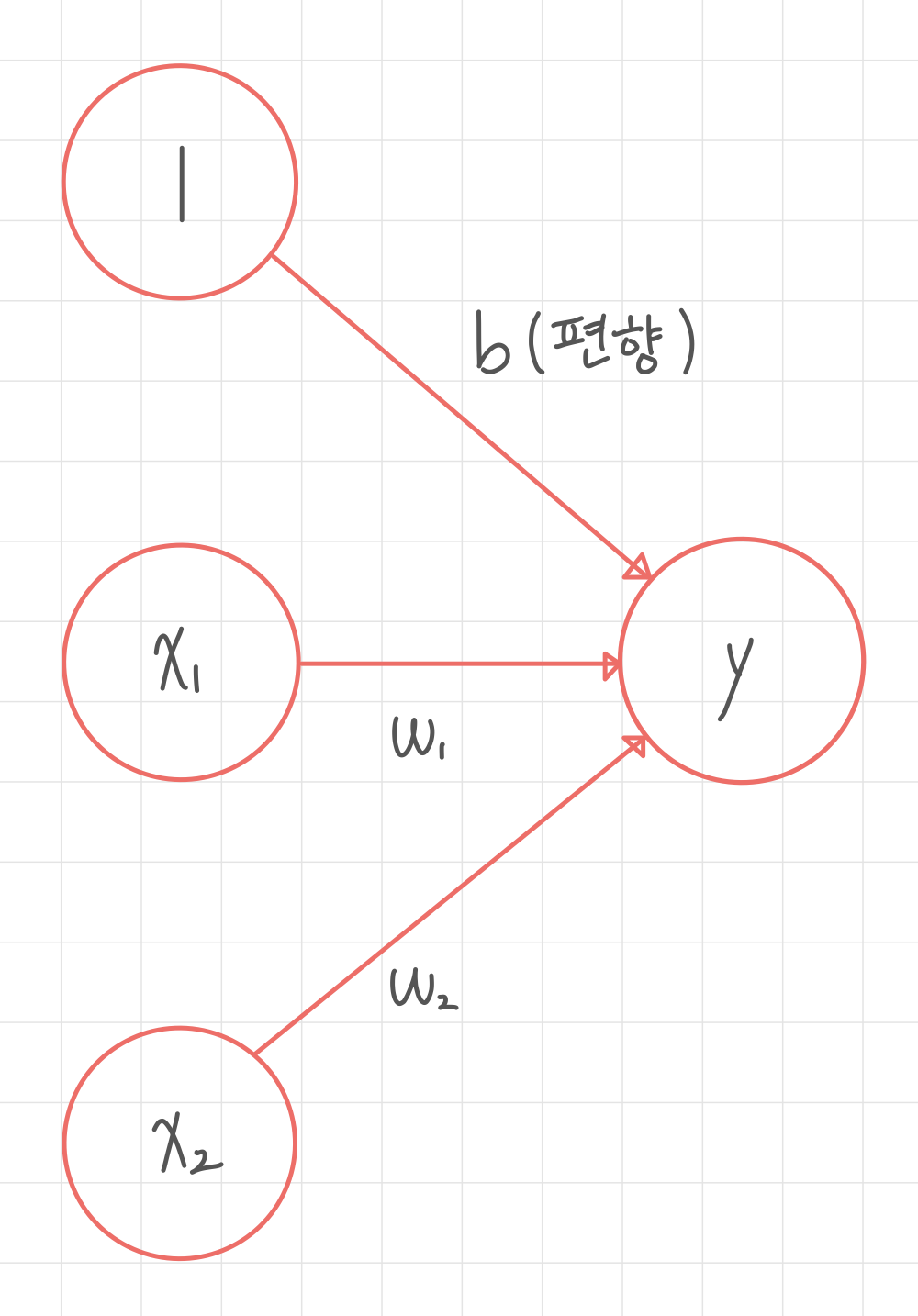
활성화 함수: sum(입력신호)->출력신호, 활성화되는지 결정

단순 퍼셉트론: 단층 네트워크에서 계단함수로 활성화 결정

다층 퍼셉트론: 신경망. 시그모이드 함수 등 부드러운 활성화 함수 사용

3.2 활성화 함수

계단 함수: 임계값 경계로 출력 변화.

#-*- coding:utf-8 -*- 
# 코드 내 한글이 있을 경우 에러가 발생해 위 코드를 추가한다.

import numpy as np
import matplotlib.pyplot as plt

# 데이터 준비
def step(x):
    return np.array(x>0,dtype=np.int) # True면 1, False면 0. int형 return
x=np.arange(-8,8,0.1) 
 # (-8, -7, ..., 0, 0.1, 0.2, ..., 7.9)
y=step(x)


# 그래프 그리기
plt.plot(x,y,label="step",color="pink")
plt.ylim(-1,2)
plt.xlabel("x")
plt.ylabel("step(x)")
plt.title("step")
plt.legend()
plt.show()

시그모이드 함수: 신경망의 대표적인 활성화 함수.

#-*- coding:utf-8 -*- 
# 코드 내 한글이 있을 경우 에러가 발생해 위 코드를 추가한다.

import numpy as np
import matplotlib.pyplot as plt

# 데이터 준비
def sigmoid(x):
    return 1/(1+np.exp(-x))  # math를 import하면 오류가 난다.
x=np.arange(-8,8,0.1) 
 # (-8, -7, ..., 0, 0.1, 0.2, ..., 7.9)
y=sigmoid(x)


# 그래프 그리기
plt.plot(x,y,label="sigmoid",color="pink")
plt.ylim(-1,2)
plt.xlabel("x")
plt.ylabel("sigmoid(x)")
plt.title("sigmoid")
plt.legend()
plt.show()

시그모이드 함수와 계단 함수

#-*- coding:utf-8 -*- 
# 코드 내 한글이 있을 경우 에러가 발생해 위 코드를 추가한다.

import numpy as np
import matplotlib.pyplot as plt

# 데이터 준비
def sigmoid(x):
    return 1/(1+np.exp(-x))
def step(x):
    return np.array(x>0,dtype=np.int)

x=np.arange(-8,8,0.1) 
 # (-8, -7, ..., 0, 0.1, 0.2, ..., 7.9)
y=sigmoid(x)
z=step(x)

# 그래프 그리기
plt.plot(x,y,label="sigmoid",color="pink")
plt.plot(x,z,label="step",color="purple",linestyle="--")
plt.ylim(-1,2)
plt.xlabel("x")
plt.ylabel("y")
plt.title("sigmoid & step")
plt.legend()
plt.show()

시그모이드의 출력값은 연속적으로 변화하는 실수이다.

시그모이드	계단
0에서 1로 연속적인 변화 0과 1 사이 실수 return	0에서 1로 급격한 변화 0,1 만 return
비선형 함수(직선X,다층 퍼셉트론에 효과적)

위 내용을 배우니 y=x같이 심플한 함수를 조금 고치면 쓸만하겠다고 생각했다.

그에 맞는 ReLU함수가 최근에 사용되고 있다.

3.3 다차원 배열의 계산

#-*- coding:utf-8 -*- 
# 코드 내 한글이 있을 경우 에러가 발생해 위 코드를 추가한다.

import numpy as np

x=np.array([[1,2,3,4],[5,6,7,8]])
y=np.array([[1,2,3],[4,5,6],[7,8,9],[10,11,12]])
z=np.dot(x,y)

print(x.shape) # (2,4)
print(y.shape) # (4,3)
print(z.shape) # (2,3)
print(z)
#[[ 70  80  90]
# [158 184 210]]

행렬 (AXB)과 행렬 (BXC)의 행렬곱은 (AXC)의 형태를 갖는다.

3.4 3층 신경망 구현하기

<신경망에서 사용하는 표기법>

<3층 신경망>

위 신경망을 보고 활성화 함수, 항등 함수, network 저장 함수, 신호 전환 함수로 구현할 수 있다.

import numpy as np

def sigmoid(x): # 활성화 함수
    return 1/(1+np.exp(-x))

def identity_function(x): # 항등함수
    return x    

def init_network(): # 가중치, 편향 초기화.  dic형인 network에 저장
    network={}
    network['w1']=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
    network['b1']=np.array([0.1,0.2,0.3])
    network['w2']=np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
    network['b2']=np.array([0.1,0.2])
    network['w3']=np.array([[0.1,0.3],[0.2,0.4]])
    network['b3']=np.array([0.1,0.2])
    return network

def foward(network,x): # 입력신호->출력신호
    w1,w2,w3 = network['w1'],network['w2'],network['w3']
    b1,b2,b3 = network['b1'],network['b2'],network['b3']

    a1=np.dot(x,w1)+b1 #0->1
    z1=sigmoid(a1)
    a2=np.dot(z1,w2)+b2 #1->2
    z2=sigmoid(a2)
    a3=np.dot(z2,w3)+b3 #2->3
    y=identity_function(a3)
    return y

network=init_network()
x=np.array([1.0,0.5])
y=foward(network,x)
print(y)

3.5 출력층 설계하기

기계학습

- 분류: 데이터가 속한 클래스 찾기, softmax 사용

- 회귀: 입력 데이터 내 연속 수치 예측하기 (이미 있는 데이터로 다음 예상하기), identity 사용

identity: 항등함수, 은닉층의 활성화 함수.

softmax: 모든 뉴런이 모든 입력 신호 전달받음, 통계적 확률 return

softmax 구현

import numpy as np

def softmax(a):
    c=np.max(a)
    exp_a=np.exp(a-c) # overflow를 막기 위해 max를 뺸다.
    sum_exp_a=np.sum(exp_a)
    y=exp_a/sum_exp_a
    return y

a= np.array([0.3,2.9,4.0])
c=np.max(a) # a의 max
y=softmax(a)
print(y)
print(np.sum(y))

[ 0.01821127  0.24519181  0.73659691] # 1.8%, 24.5%, 73.7%
1.0 # 총합 100%

결과: 2번째 원소가 가장 확률이 높다!

a의 관계대로 softmax의 결과가 나온다.

따라서, 신경망으로 분류시 출력층의 softmax는 생략한다.